Cómo resolver integrales indefinidas paso a paso
Dada una función f (x), se dice que la función F (x) es primitiva de ella si se verifica que F'(x) = f (x). La operación que consiste en obtener el primitivo de una función dada se denomina integración, que es el inverso de la derivación.
De esta definición se deduce que la función f (x) tiene infinitos primitivos, ya que si F (x) es primitiva de f (x), también lo será cualquier otra función definida como G (x) = F (x) + C, siendo C un valor constante.
El conjunto de todas las primitivas de una determinada función f (x) se denomina la integral indefinida de la función, y se denota genéricamente como
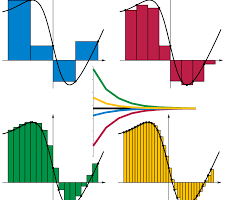
Las primitivas de una función forman una familia de curvas desplazadas verticalmente unas de otras. Así, la función f (x) = x tiene infinitas primitivas que difieren en una constante, tal como se muestra a la derecha.
Propiedades de las primitivas
- Aplicando las propiedades de la derivación, es posible determinar algunas propiedades comunes de la integración. Las siguientes propiedades de linealidad sirven para descomponer las integrales complicadas en otras más simples:
- La integral de la suma (o diferencia) de dos funciones es igual a la suma (o diferencia) de las integrales de cada una de ellas.
- La integral del producto de una constante por una función es igual al producto de la constante por la integral de la función.