Derivadas de funciones

El concepto de una derivada de una función matemática está estrechamente relacionado con la noción de límite. Así, la derivada se entiende como la variación que la función experimenta instantáneamente, es decir, entre cada dos puntos de su dominio suficientemente cercanos entre sí. La idea de instantaneidad transmitida por la derivada tiene múltiples aplicaciones en la descripción de los fenómenos científicos, tanto naturales como sociales.

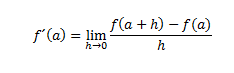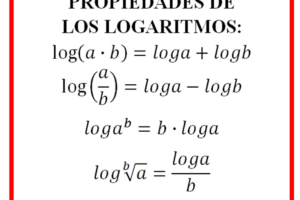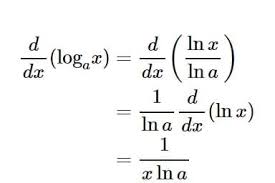
Función derivada

Si f es una función continua definida en un dominio A, la función derivada de f se define en el punto a del conjunto A y se denota por f'(a), en el valor del límite siguiente:

Si llamamos h= x-a, también podemos escribir la definición de la siguiente manera:

Variación de una función

Dada una función f (x), se define la variación de la función entre dos puntos de su dominio x1 y x2, siendo x1 < x2, a la diferencia f (x2) - f (x1). Cuando esta diferencia es positiva, la función aumenta en el punto; si es negativa, la función disminuye.

En relación con este concepto, se denomina variación media de una función f (x) en un intervalo [a, b] al siguiente cociente:

El valor de este cociente coincide con la pendiente de la recta que pasa por los puntos de coordenadas (a, f (a)) y (b, f (b)).

Cuando los dos puntos del intervalo [a,b] están suficientemente próximos entre sí, el cociente anterior indica la variación instantánea de la función. En tal caso, el valor de b podría expresarse como b = a + h, siendo h un valor infinitamente pequeño.

Derivada de una función en un punto

Dada una función f (x), y considerada un punto a de su dominio, se denomina derivada de la función en ese punto, denotada como f =(a), hasta el siguiente límite:

Entrada Relacionada: Proyecciones matemáticas

Este límite también puede expresarse de las dos formas alternativas siguientes:

Derivadas laterales

Como sucedía con los límites, se pueden definir los conceptos de derivadas laterales de una función en un punto.

Dada una función f (x) y considerado un punto a de su dominio de definición, se define su derivada por la derecha, y se denota como f =(a+), al límite siguiente: