Máximos y mínimos de una función de dos variables
La parte más difícil de este tipo de problema es encontrar la expresión analítica de la función. En primer lugar debemos tener en cuenta que la función debe ser continua. Una vez hecho esto debemos:
- Buscar las condiciones que nos da la declaración.
- Buscamos la relación entre las variables x e y.
- Para despejar una de ellas.
- Debemos buscar la expresión analítica que debemos optimizar en base a las expresiones del enunciado del problema.
- Derivamos e igualamos a cero para encontrar los extremos.
- Calculamos la segunda derivada para comprobar el resultado y saber si hemos obtenido un máximo o un mínimo.
Máximos y mínimos de una función de dos variables ejercicios resueltos
Obtener el triángulo isósceles de área máxima inscrito en un círculo de radio 12 cm.

Función a optimizar:
![]()
Relacionamos las variables:
![]()
Sustituimos en la función:
![]()
Derivamos, igualamos a cero y calculamos las raíces.

![]()
![]()
![]()
Realizamos la derivada segunda para comprobar el resultado obtenido

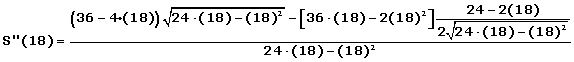
Podemos observar que el resultado sera negativo:
![]()
Así, el criterio de la segunda derivada establece que "si la segunda derivada es inferior a cero (negativa), entonces la función tiene un máximo relativo. En conclusión, para la altura máxima de 18, hay un máximo relativo.
Contenido