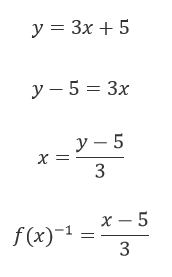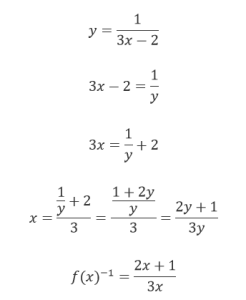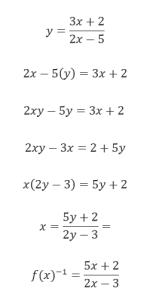Función inversa
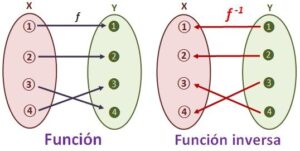
Sea f una función que asigna a los elementos de un primer conjunto (conjunto inicial X) un elemento de un segundo conjunto (conjunto final Y). La función inversa (o función recíproca) de f (denotada por f-1) es la que hace el camino inverso, asignando a los elementos de Y elementos de X.
Formalmente, diremos que f-1 es la inversa de f si:
También podemos definir una función inversa a partir de la composición de las funciones. f-1 es la inversa de f y f-1 si la composición de f da la identidad de la función.
Para que una función f tenga el inverso necesariamente debe ser inyectiva.
Además, tanto f como f-1 deben ser biectivas.
Propiedades
Los gráficos de una función f y su inversa f-1 son simétricos con respecto a la bisectriz del 1er y 3er cuadrante.
Entonces, si un punto (a , b) pertenece a la función f, el punto (b , a) pertenecerá a su inversa f-1.
- El dominio de f-1 es el camino de f.
- El dominio de f-1 es la trayectoria de f.
El inverso de la función inversa es la función misma.
El inverso de la composición de las funciones f y g (g o f).
Método de cálculo de la función inversa
Tenemos la función y = f(x), realizamos los siguientes pasos:
Despejamos la variable x en función de y. Por ejemplo:
Las variables x y y se intercambian y la función resultante será la función inversa. Por ejemplo:
Ejemplos de Función inversa
- f (x) = 3x + 5
- f (x) = 1 / (3x – 2)
- f (x) =(3x + 2) / (2x – 5)
Contenido