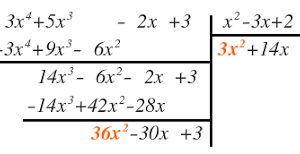Límite infinito entre infinito

Al considerar el cociente entre polinomios cuando la variable x tiende a ser infinita, el límite puede determinarse considerando el grado de los polinomios. Esta situación puede generalizarse para cualquier cociente entre funciones considerando el grado de ambas funciones. Veamos entonces con los siguientes ejemplos cómo determinar este tipo de límites.

Límite infinito entre infinito

El limite presenta una indeterminación pero considerando que el grado de la función en el numerador es igual y el grado del denominador es igual a
Si consideramos , este límite presenta una indeterminación pero considerando que el grado de la función en el numerador es exponencial y el grado del denominador es igual a 7 entonces
$\lim_{x \to \infty} \frac{x + 100}{\ln(x) + 20} = \frac{\infty}{\infty}$ , este límite presenta una indeterminación pero considerando que el grado de la función en el numerador es igual a 1 y el grado del denominador es logarítmico entonces

Límite que involucra una función radical

, este límite presenta una indeterminación pero considerando que el grado en ambos miembros de la fracción es , entonces dividimos el numerador y el denominador por