Multiplicación de matrices

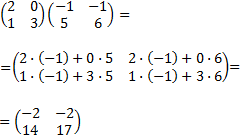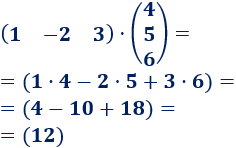
Producto de la matriz

El producto de la matriz requiere una condición previa muy restrictiva: si A y B son dos matrices, sólo pueden multiplicarse si el número de columnas de la primera matriz coincide con el número de filas de la segunda. Se dice en este caso que A y B son multiplicables.
El resultado es una matriz que tiene tantas filas como la primera y tantas columnas como la segunda.

Así, si C es la matriz del producto A-B, el elemento cij se obtiene de la siguiente manera:

• Selecciona la fila i de la primera matriz y la columna j de la segunda.
• Multiplicar el primer elemento de la fila por el primer elemento de la columna seleccionada. Haga lo mismo con el segundo, tercero, ..., hasta el último elemento de la fila y columna seleccionadas.
• Finalmente, sume todos los productos hechos. El resultado de esta suma es el elemento buscado.

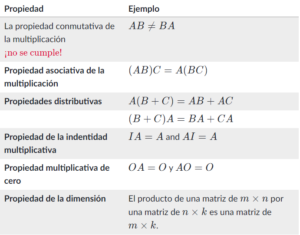
Propiedades de las matrices

Ejemplo de Multiplicación de matrices

Producto de dos matrices de dimensión 2×2:

Para multiplicar los vectores de fila y columna, tienen que ser de la misma dimensión. Esto implica que el número de columnas de la matriz A debe coincidir con el número de filas de la matriz B.

Es decir, para calcular el producto A-B la dimensión de A debe ser mxn y la dimensión de B debe ser nxk. El producto de la matriz A-B es de dimensión mxk.