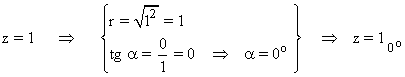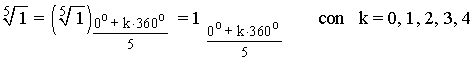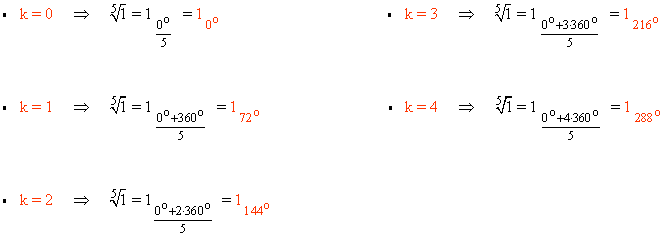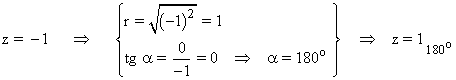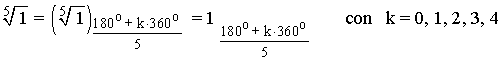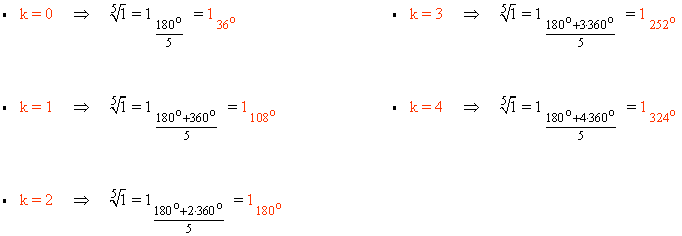Raíces de números complejos
Dejemos que Ra sea un número complejo y consideremos otro complejo R'a', de tal manera que
Ra = (R' a' )n = ((R' )n )n a'
Esto es equivalente a (R')^n = R, o lo que es lo mismo, que R'=n√R, y que
nα'= α+k*360°⇐⇒ α'= α⁄n + k*360/n, donde K es un número arbitrario. Es decir,
n^√Rα = (n^√R) α+k*360°/n
Cuando se representa la n-ésima raíz de un número complejo, ya que todas tienen el mismo módulo, se cumple que
- Sus respectivas fijaciones están en un círculo de radio igual al módulo de la arcilla.
- Los afijos de la enésima raíz son los vértices de un polígono regular de n lados inscrito en ese círculo.
Raíces de números complejos ejercicios resueltos
En primer lugar pasamos el número complejo a forma polar:
Sabemos que la tangente de un ángulo vale 0 en 0o y 180o . Como el afijo de z es (1, 0) el ángulo del número complejo es 0o . A continuación aplicamos la fórmula para encontrar las raíces quintas de z:
En primer lugar pasamos el número complejo a forma polar:
Sabemos que la tangente de un ángulo vale 0 en 0o y 180o . Como el afijo de z es (-1, 0) el ángulo del número complejo es 180o . A continuación aplicamos la fórmula para encontrar las raíces quintas de z:
Contenido