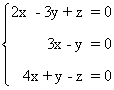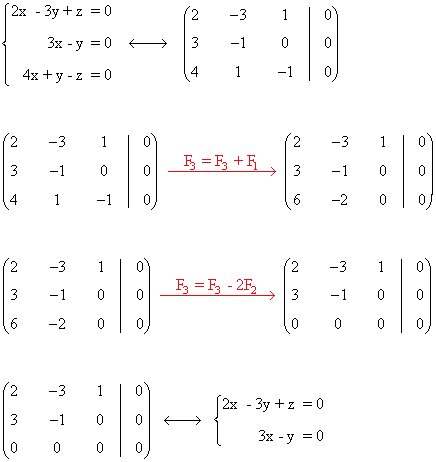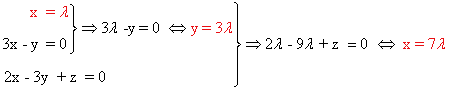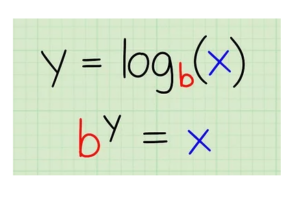Ecuaciones lineales homogéneas

Decimos que un sistema de ecuaciones es homogéneo cuando todos los términos independientes son cero.

Ecuaciones lineales homogéneas

La condición necesaria y suficiente para que un sistema homogéneo tenga soluciones distintas de la trivial es que el rango de la matriz de coeficientes sea menor que el número de incógnitas, o en otras palabras, que el determinante de la matriz de coeficientes sea cero.

Ejemplo de ecuaciones lineales homogéneas

Una ecuación diferencial de primer orden que se puede llevar a escribir de la forma:

se denomina ED de primer orden homogénea.

Procedimiento:

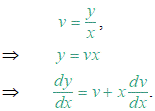
Para resolver una ecuación diferencial homogénea se procede a efectuar las siguientes sustituciones:

Ejemplo

La función es homogénea de grado .
Las funciones , , son homogéneas de grado 0.
Las funciones , , son homogéneas de grado 2.

Propiedades básicas

Si una ecuación lineal diferencial es homogénea, el conjunto de soluciones formará un espacio vectorial de n dimensiones (siendo n el orden de la ecuación diferencial). En particular, una ecuación lineal diferencial admitirá soluciones de la forma:

Aplicaciones

A menudo, la resolución de una ecuación diferencial ordinaria puede abordarse resolviendo primero la "versión homogénea" de esa ecuación diferencial, que consiste en una ecuación en la que se han eliminado las sumas necesarias hasta obtener una ecuación homogénea. En los casos de mayor interés práctico, el espacio de solución de una ecuación diferencial lineal forma un espacio afín que puede construirse a partir del espacio vectorial asociado al conjunto de soluciones de la "versión homogénea".