Tipos de sólidos de revolución
Los sólidos de la revolución pueden clasificarse según la curva que los genera:
Esfera
Basta con girar un semicírculo alrededor de un eje que será el diámetro de la esfera de radio R. Su volumen es:
Vesfera = (4/3)πR3
Cono
Para obtener un cono de altura H y radio R, la superficie a rotar es un triángulo rectángulo, alrededor del eje axial que pasa por una de las patas. Su volumen es:
Vcono = (1/3)πHR2
Cilindro
Girando un rectángulo alrededor de un eje axial que pasa por uno de los lados, que puede ser el lado corto o el largo, se obtiene un cilindro circular recto de radio R y altura H, cuyo volumen es
Cilindro = πR2H
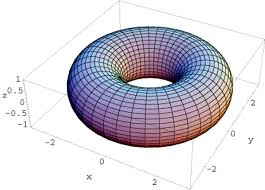
Toroide
El toroide tiene forma de dona. Se obtiene rotando una región circular alrededor de una línea recta en el plano que no intersecta el círculo. Su volumen viene dado por:
Vtoroide = 2πa2R
Métodos para calcular el volumen de un sólido de revolución
En el cálculo integral estos dos métodos son frecuentes:
- Discos y arandelas
- Cascarones
Método de disco o arandela
Cuando se corta un sólido de revolución la sección transversal puede ser un disco, si el sólido es sólido o puede ser una especie de arandela (un disco con un agujero en el medio), si es un sólido hueco.
Supongamos que una región plana gira alrededor del eje horizontal. De esa región plana tomamos un pequeño rectángulo de ancho Δx, que está hecho para rotar perpendicularmente alrededor del eje axial.
La altura del rectángulo está entre la curva más exterior R(x) y la más interior r(x). Corresponden al radio exterior e interior respectivamente.
Al hacer esta rotación, se genera una arandela de volumen ΔV, dada por:
ΔV = Volumen completo - volumen del agujero (si lo hay)
Recordando que el volumen de un cilindro circular recto es π. radio2 x altura, tenemos:
ΔV = π [R2(x) - r2(x)] Δx
El sólido puede dividirse en una multitud de porciones de pequeño volumen ΔV. Si los sumamos todos, tendremos el volumen completo.
Para ello, hacemos que el volumen de ΔV tienda a 0, así que Δx también se vuelve muy pequeño, convirtiéndose en un diferencial de dx.
De esta manera tenemos una integral:
V = ∫ab π [R2(x) - r2(x)] dx
En caso de que el sólido sea sólido, entonces la función r (x) = 0, el trozo del sólido que se genera es un disco y el volumen permanece:
V = ∫ab πR2(x) dx
Cuando el eje de la revolución es vertical, las ecuaciones anteriores toman la forma:
V = ∫ab π [R2 (y) - r2 (y)] dy y V = ∫ab πR2(y) dy
Método de capas
Como su nombre indica, este método consiste en suponer que el sólido está compuesto por capas de espesor diferencial. La capa es un tubo delgado que se origina por la rotación de un rectángulo paralelo al eje de rotación.
Ejercicio resuelto
Encuentra el volumen generado por la rotación de la región plana entre las curvas:
y = x2; y=0; x=2
Alrededor del eje Y.
Solución
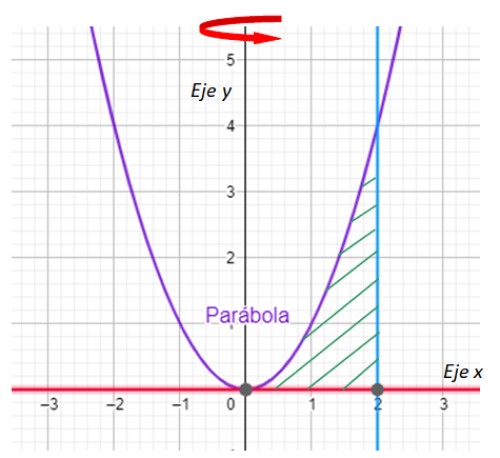
Lo primero que debemos hacer es trazar la región que va a generar el sólido de la revolución y señalar el eje de rotación. Lo tenemos en el siguiente gráfico:
Ahora buscamos las intersecciones entre la curva y = x2 y la línea x = 2.
En la gráfica es fácil notar que la parábola y la línea se intersectan en el punto (2,4), lo que se corrobora sustituyendo x = 2 por y = x2.
Entonces, se elige uno de los métodos para calcular el volumen, por ejemplo el método de la capa con eje de revolución vertical:
V = ∫ab 2π p(x)h(x)dx
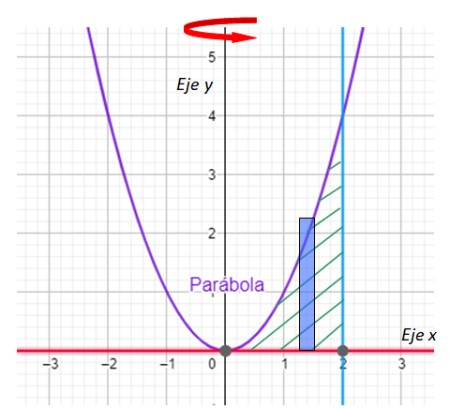
Paso 1: Dibujar el rectángulo
Importante: En el método de capas, el lado largo del rectángulo es paralelo al eje de rotación.
Paso 2: Determinar p(x)
El radio de la capa es x
Paso 3: Determinar h(x)
La altura del rectángulo está determinada por la parábola x2.
Paso 4: Establecer y resolver la integral del volumen
La variable de integración es x, que varía entre 0 y 2, por lo que tenemos los límites de integración. Sustituyendo las expresiones por p(x) y h(x):
Contenido