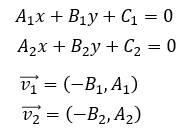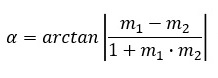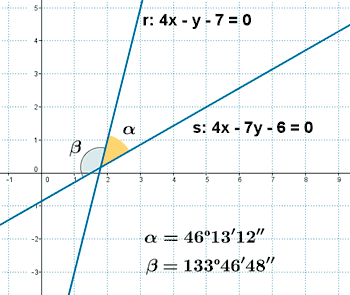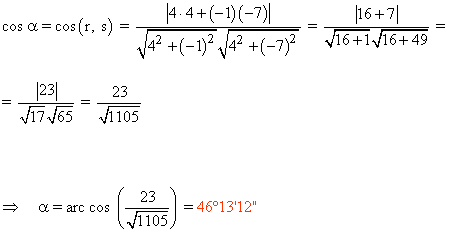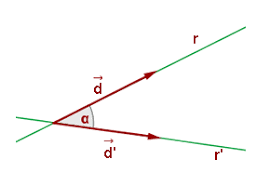
¿Cómo se calcula el ángulo entre dos rectas?
El ángulo entre dos líneas que se cortan en el plano cartesiano puede calcularse por dos procedimientos: a partir de sus vectores direccionales o de sus pendientes.
El ángulo se puede obtener a través del producto escalar de sus vectores directores:
Podemos obtener vectores directores de cada línea de los coeficientes A y B de sus respectivas ecuaciones establecidas en su forma general:
En el producto escalar, el numerador se obtiene por los determinantes de las matrices del rango 2:
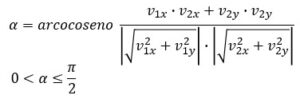
Y el ángulo se obtiene por el arcocoseno, (la función inversa del coseno), una vez que éste se ha despejado en la expresión del producto escalar. En el denominador, el módulo de los vectores directores se encontrará aplicando el teorema de Pitágoras a sus componentes:
El otro procedimiento, más sencillo, es a partir de sus pendientes, que son los coeficientes m1 y m2 de la x de las ecuaciones de las rectas secantes puestas en forma explícita u ordinaria:
Tomar siempre el ángulo más pequeño de los dos pares que se forman cuando se cortan las dos rectas, siendo 0 < α ≤ π/2.
Ángulo entre dos rectas ejercicio resuelto
Calcula el ángulo entre las líneas r ≡ 4x - y - 7 = 0 y s ≡ 4x - 7y - 6 = 0
Contenido