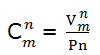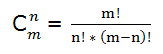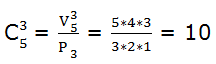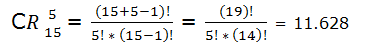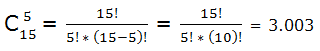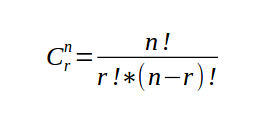
Combinaciones sin repetición

Las combinaciones sin repetición o las combinaciones ordinarias de m elementos tomadas de n en n (de orden n) son los diferentes grupos de n elementos diferentes que se pueden hacer con los m elementos que tenemos, de modo que dos grupos difieren en algún elemento y no en el orden de colocación. Se representa por Cm,n. (n≤m).

Combinaciones sin repetición

Definición: Son las diferentes formas de organizar o agrupar los elementos de un conjunto sin tener en cuenta el orden de su ubicación.

a) Dos combinaciones se consideran diferentes, sólo por los elementos que las componen.
b) Las combinaciones no están influenciadas por el orden en que se colocan los elementos.
c) En las combinaciones, los elementos de un mismo grupo no se repiten

La fórmula para calcular el número de combinaciones de "n" elementos diferentes tomada de "k" en "k con k ≤ n ,es: nCk = n! / k!(n-k)!

n = Número de elementos a elegir
k = Número de elementos en cada combinación

¿Cómo calcular la combinatoria sin repetición?

En las combinaciones sin repetición, como su nombre indica, ningún elemento puede ser repetido.

Obligatoriamente n <= m.

Las combinaciones sin repetición se representan por o también por .

Para calcular el número de grupos que se pueden formar se aplica la fórmula.

También se pueden calcular las combinaciones aplicando factoriales:

Veamos un ejemplo: con las 5 vocales cuantos grupos de 3 letras podemos formar teniendo en cuenta que ninguna letra se puede repetir y que el orden no importa.

Entrada Relacionada: Área de un paralelogramo con vectores