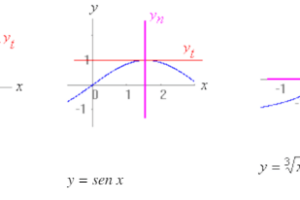
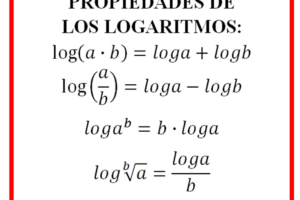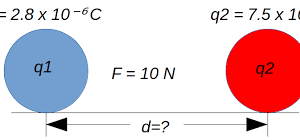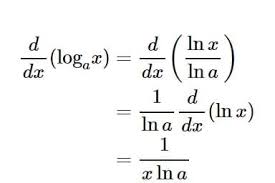Inecuaciones racionales
Inecuaciones algebraicas en las que sus dos miembros están relacionados por los signos: mayor, menor, mayor o igual o menor o igual. La solución de una inequidad es el conjunto de valores de la variable que la verifica, donde la solución se expresa mediante una representación gráfica y/o mediante un intervalo.
Para dar solución a una desigualdad es necesario tener en cuenta que:
- Una inequidad se verifica sólo para algunos valores de las variables.
- Los valores numéricos para los que se verifica la desigualdad son las soluciones de la misma.
- La solución de una inequidad consiste en encontrar los valores numéricos para los cuales la desigualdad es verdadera.
Regla general para resolver una inecuación
Sigue el mismo procedimiento que para resolver una ecuación (eliminar denominadores, términos, agrupaciones, etc.), pero hay que tener en cuenta, al multiplicar o dividir por cantidades negativas, que hay que cambiar la dirección de la desigualdad para que el resultado no varíe.
Método para resolver desigualdades fraccionales
Las desigualdades fraccionales o racionales tienen incógnitas tanto en el numerador como en el denominador y se resuelven de manera similar a las del segundo grado, pero hay que tener en cuenta que el denominador no puede ser cero.
Para encontrar la solución hay que descomponer factorialmente el numerador y el denominador de los polinomios, aplicando Ruffini, complicidad de los cuadrados, etc... el método que se considere más apropiado o que se encuentre mejor. Una vez descompuesto nunca se simplifica ya que se podrían perder soluciones. Después se procede como con las desigualdades de grado superior a uno, ya que es básicamente para averiguar el signo final que va a tener un cociente de productos binomiales.