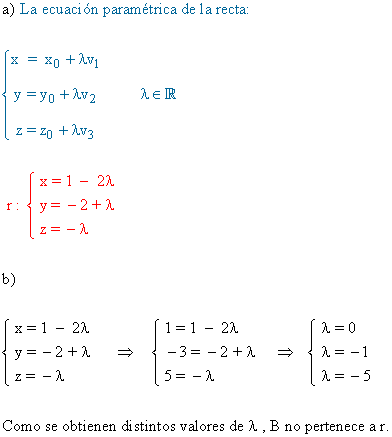Ecuación de la recta en el espacio
Una línea r se determina cuando conocemos un punto de ella A(x1, y1, z1) y un vector director v(v1, v2, v3)
ECUACIÓN VECTORIAL DE LA RECTA
El vector de posición del punto A se llama a. Tomamos un punto genérico en la línea X.
Llamamos al vector de posición del punto X
Se observa en la figura que el vector AX puede ser un vector director de la línea.
En la figura vemos que x = a + AX, AX= t. v
Por lo tanto tenemos x = a + t. v que es la ecuación vectorial
En coordenadas será (x, y, z) = (x1, y1, z1) + t. (v1, v2, v3)
Ejemplo La ecuación vectorial de la recta que pasa por (2, 1, - 3) y tiene un vector director v (4, - 1, 5) es (x, y, z) = (2, - 1, - 3) + t. ( 4, - 1, 5)
ECUACIONES PARAMÉTRICAS DE LA RECTA
De la ecuación vectorial que tenemos:
x = x1 + t. v1
y = y1 + t. v2
z = z1 + t. v3
Ejemplo Las ecuaciones paramétricas de la recta anterior son:
x = 2 + 4t
y = 1 - t
z = - 3 + 5t
Dando valores al parámetro t, obtenemos puntos en la línea. Así que, si t = 2, obtenemos x = 10,
y = - 1, z = 7, por lo que (10, - 1, 7) es un punto en esa línea.
LA ECUACIÓN CONTINUA DE LA RECTA
A partir de las ecuaciones paramétricas despejamos el parámetro t, e igulamos:
(x - x1) / v1 = (y - y1) / v2 = (z - z1) / v3
Ejemplo La ecuación continua de la línea anterior es
(x - 2) / 4 = (y - 1) / - 1 = (z + 3) / 5
ECUACIONES DE RECTA REDUCIDAS
Están dadas por la intersección de dos planos
Ax + By + Cz + D = 0
A'x + B'y + C'z + D'= 0
Este sistema es compatible indefinidamente, tiene infinitas soluciones, que son los puntos de la línea, siendo estructurado de forma paramétrica.
Ejemplos de Ecuación de la recta en el espacio
Contenido