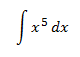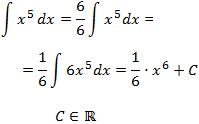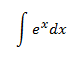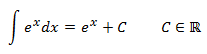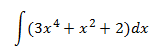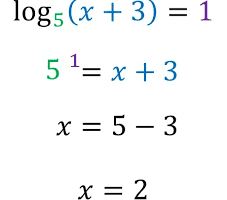
Fórmulas de integrales
Las llamamos integrales inmediatas ya que el método que utilizaremos consiste en, teniendo en cuenta los derivados elementales, conseguir en él una función multiplicada por su derivado. De esta manera, por la regla de la cadena, lo primitivo es esta función. Por lo tanto, necesitamos conocer los derivados elementales, las reglas de derivación y la regla de la cadena y las propiedades de las integrales.
Fórmulas de integrales
Integrales inmediatas ejercicios resueltos
Ejercicio 1
Aplicaremos la propiedad "una constante puede entrar o salir de la integral".
Sólo necesitamos un 6 multiplicando en la integral para tener la derivada de x6. Multipliquemos y dividamos la integral por 6 para introducir un 6 en el radicando:
Ejercicio 2
No tenemos que hacer ninguna operación para resolver esta integral porque e^x es el derivado de e^x. Sólo tenemos que recordar escribir la constante de integración C.
Ejercicio 3
Aplicamos la propiedad de que la integral de la suma es la suma de las integrales. Así, podemos descomponer la integral como una suma de integrales más simples.
Contenido