Fracciones impropias a mixtas

$fracciones impropias$

Una fracción impropia tiene su numerador (número superior) mayor o igual a su denominador (número inferior)

Características de las fracciones impropias

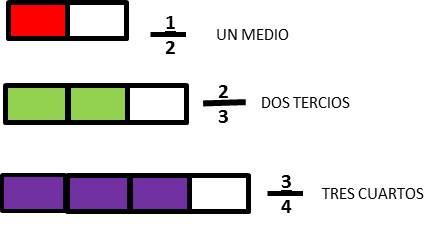
En las fracciones impropias el numerador (el número en la parte superior de la fracción) es siempre mayor que su denominador (el que está en la parte inferior), por lo que también puede expresarse como la combinación entre un número entero y un número fraccionario y menos de 1.

Hablamos de "combinación", porque en la escritura aparecen así: el número entero y a su derecha el número fraccionario. Aunque formalmente se debe escribir un signo "+" entre los dos, esto no suele hacerse.

Esos números compuestos por un entero y una fracción se llaman números mixtos, y se ven a menudo en los signos de las tiendas que venden productos por peso.

Por ejemplo, en una tienda de helados, casi nadie elegirá pedir 5/2 de un kilo de helado (y mucho menos en una proporción mayor, como 25/10), pero seguramente pedirán 2 ½, es decir, "dos kilos y medio" de helado.

El ejercicio de transformar una fracción impropia en un número mixto es simple: hay que descomponer el numerador para que sea divisible por el denominador, lo que da como resultado un número entero (en el ejemplo, 4/2=2), la fracción restante (en este caso ½) será la fracción.

A efectos del análisis matemático, es inútil expresar una fracción impropia como el número de unidades que tiene y el cociente menor que uno, porque lo que importa es cada número por separado: las operaciones entre fracciones, así como las que combinan fracciones y números enteros, son mucho más sencillas siempre que se trabaje con fracciones impropias.

Entrada Relacionada: Ecuaciones matriciales

Aunque las operaciones entre fracciones correctas e incorrectas se realizan de la misma manera, hay ciertas características diferenciales en ambos casos, como el hecho de que una multiplicación entre fracciones incorrectas da como resultado una fracción impropia.

Fracciones impropias

La división entre las fracciones impropias depende precisamente de qué número se coloca como dividendo (numerador) y cuál como divisor (denominador): si el primero es mayor que el segundo, será una fracción impropia, mientras que si el segundo es mayor, será su propia fracción.

Un caso particular de fracciones impropias son las que dan lugar a una división en la que no hay resto, es decir, una en la que el numerador es un múltiplo del denominador y luego es un número entero: son las llamadas fracciones aparentes.