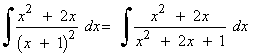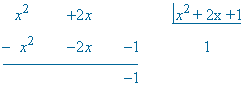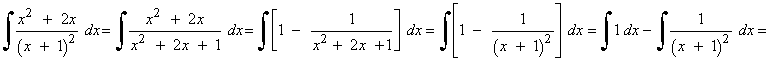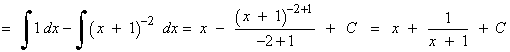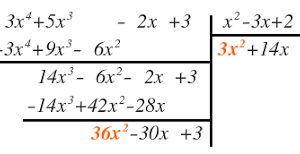Integrales con raíz en el denominador

Las funciones algebraicas no racionales son las que contienen radicales. Sólo unas pocas de ellas pueden ser integradas en términos de funciones elementales. En algunos casos, mediante la sustitución de una nueva variable, estas funciones pueden transformarse en funciones equivalentes que son racionales o directamente integradas (integración directa). El método de integración por racionalización es un método de integración de una función no racional que consiste en sustituir la variable por una nueva de manera que el resultado sea una función racional.

Integrales con raíz en el denominador

Una función racional S(x) definida en un intervalo cerrado [a , b] se puede expresar en la forma:

Siendo P(x) y Q(x) dos polinomios primos entre sí y de forma que Q(x) no se anula en el intervalo [a , b].

En el caso de que el grado del numerador sea mayor que el del denominador, la función puede expresarse como suma de un polinomio G(x) y de una función racional cuyo numerador sea de grado inferior que el denominador, es decir:

Suponiendo que ya tenemos S(x) en esta última forma y que el polinomio Q(x) admite una descomposición del tipo:

Donde a₁, a₂, … son raíces reales de multiplicidad a,b,..., … respectivamente y b₁ ± c₁.i , b₂ ± c₂.i … son raíces imaginarias conjugadas de multiplicidad h, k, … respectivamente, entonces existe la descomposición en fracciones simples del tipo:

Se demuestra que esta descomposición existe y que es única.

La obtención de los coeficientes indeterminados puede hacerse de distintas formas. Así, por ejemplo, escrita a priori, la fórmula de descomposición, con coeficientes indeterminados en los numeradores del segundo miembro, se quitan denominadores multiplicando ambos miembros por Q(x). basta entonces igualar coeficientes de las mismas potencias de x en la igualdad que resulta para formar un sistema lineal de ecuaciones de solución única de las incógnitas buscadas, A_j, B_j, C_j.

Entrada Relacionada: División de integrales

En algunos casos puede aplicarse un método sencillo que consiste en ir dando a x cada uno de los valores que son raíces del denominador.