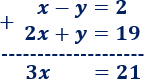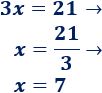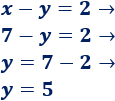Método de reducción ejercicios resueltos paso por paso

Un sistema de ecuaciones es un conjunto de dos o más ecuaciones con varias incógnitas en las que queremos encontrar una solución común. Esta vez resolveremos un sistema de dos ecuaciones lineales con dos incógnitas. Una ecuación lineal con dos incógnitas es una igualdad del tipo ax+by=c, donde a, b y c son números, y «x» e «y» son las incógnitas. Una solución es cualquier par de números que cumpla con la ecuación.

Método de reducción

Consiste en multiplicar una o ambas ecuaciones por algún número para obtener un sistema en el que los coeficientes de x o y sean iguales y de signo opuesto, para eliminar la incógnita al sumar las dos ecuaciones.

Método de reducción ejercicios resueltos paso por paso

Comprueba si ambas ecuaciones se pueden sumar o restar de tal manera que se elimine una de sus variables. Si no es posible eliminar directamente, debemos multiplicar una o ambas ecuaciones por algún valor, de modo que en ambas ecuaciones tengamos alguna variable con el mismo coeficiente.
Una vez que se tengan variables con el mismo coeficiente, éstas se podrán restar y así se eliminará una de las variables.
En la ecuación obtenida, debemos eliminar la variable.
Sustituimos la variable en una de las dos primeras ecuaciones para obtener el valor de la otra variable.

Ejemplo de método de reducción

Elegimos una pregunta para eliminar: la y.
Sus coeficientes son -1 en la primera ecuación y 1 en la segunda. Como son iguales y de signo contrario, sumaremos las ecuaciones para que desaparezca lo desconocido.

Sumamos las ecuaciones para eliminar la y:

Entrada Relacionada: Funciones de segundo grado