¿Qué es el método gráfico de un sistema de ecuaciones?
Como trabajaremos con sistemas de dos ecuaciones lineales con dos incógnitas x e y , la gráfica de cada ecuación es una recta. Como resultado, la intersección de las gráficas es un único punto
(a,b) y la solución del sistema es x=a e y=b.
Sin embargo, veremos dos ejemplos de casos especiales: un sistema sin solución (líneas paralelas) y un sistema con soluciones infinitas (líneas iguales).
Obviamente, para aplicar el método gráfico debemos saber cómo representar los gráficos de las líneas. Lo haremos uniendo puntos previamente calculados.
Terminaremos con un sistema de dos desigualdades (o desigualdades). En este caso, la solución del sistema es la intersección de dos regiones del plano.
Recuerda que la solución de un sistema de ecuaciones son los valores de las incógnitas x e y que hacen que todas las ecuaciones del sistema se verifiquen.
Pasos para resolver un sistema de ecuaciones por el método gráfico
El proceso de resolución de un sistema de ecuaciones mediante el método gráfico se resume en las siguientes fases:
- Despeja lo desconocido y en ambas ecuaciones.
- Construye, para cada una de las dos funciones de primer grado obtenidas, la tabla de valores correspondientes.
- Ambas líneas se representan gráficamente en los ejes de coordenadas.
En este último paso hay tres posibilidades:
-
- Si se cortan ambas rectas, las coordenadas del punto de corte son los únicos valores de las incógnitas x e y. Se determina el sistema compatible.
- Si ambas líneas son coincidentes, el sistema tiene infinitas soluciones que son las respectivas coordenadas de todos los puntos de esa línea donde ambas coinciden. Sistema compatible indeterminado.
- Si ambas líneas son paralelas, el sistema no tiene solución. Sistema incompatible.
Ejemplo de un sistema de ecuaciones resuelto por el método gráfico
Entre Ana y Sergio tienen 600 euros, pero Sergio tiene el doble de dinero que Ana. ¿Cuánto dinero tiene cada uno?
Llamemos a la x al número de euros de Ana y a la y de Sergio. Expresemos las condiciones del problema por medio de ecuaciones: Si ambos tienen 600 euros, esto nos da la ecuación x + y = 600. Si Sergio tiene el doble de euros que Ana, tendremos y = 2x. Ambas ecuaciones juntas forman el siguiente sistema:
x + y = 600
2x - y = 0
Para resolver el sistema por el método gráfico aclaramos lo desconocido y en ambas ecuaciones y tendremos
y = -x + 600
y = 2x
Ahora, para representar ambas líneas, calculemos sus tablas de valores:
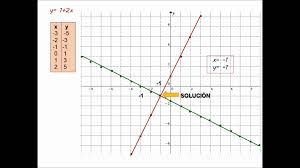
Con estas tablas de valores para las dos líneas y eligiendo las escalas apropiadas en los ejes OX y OY, ya podemos representarlos gráficamente:
Si miramos el gráfico, vemos claramente que las dos líneas están cortadas en el punto (200, 400), entonces la solución del sistema es x = 200 y y = 400. Por lo tanto, la respuesta al problema planteado es que Ana tiene 200 euros y Sergio tiene 400 euros, es decir, el mismo resultado, obviamente, que habíamos obtenido con los tres métodos analíticos.
Contenido