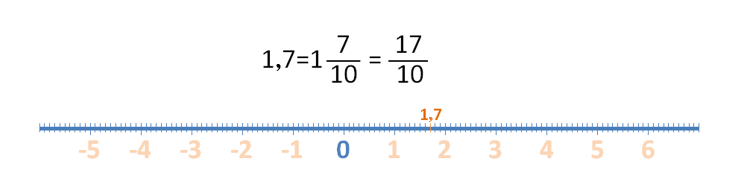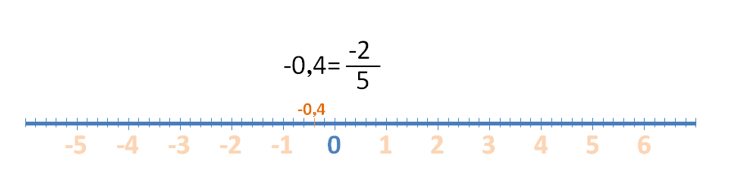
Representación de números naturales

Como hemos visto hay diferentes tipos de números, entre ellos encontramos los naturales, enteros y racionales. Es importante aprender a representar estos tipos de números de forma gráfica, para poder tener una mejor comprensión no sólo de ellos, sino también entender mucho mejor las operaciones que se pueden realizar entre ellos. La línea numérica no es más que una línea recta en la que los números están dispuestos de cierta manera.

Cómo ubicar los diferentes números en la recta numérica

Ubicar números naturales (N) en la recta numérica:

Empezaremos por los más sencillos, los números naturales (N), que son los que utilizamos para contar.

Para empezar, marcamos un punto en la recta al que llamamos 0 y la dividimos en segmentos, todos de la misma longitud. Cada uno representa una unidad, que separa un número entero del siguiente. Así:

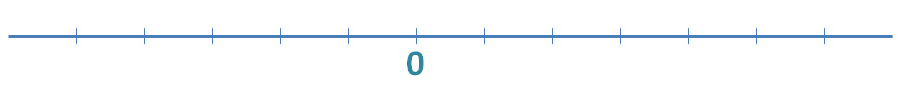
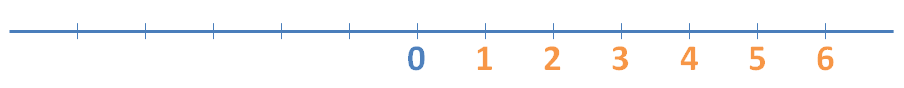
Recta dividida en segmentos de la misma longitud con un punto al que llamamos 0.

Recta dividida en segmentos del mismo tamaño con la ubicación de los números naturales en cada uno de sus extremos, a la derecha del punto 0.

Ubicar números enteros (Z) en la recta numérica:

Los números enteros (Z), se representan de la misma forma que los naturales pero también incluyen el sentido contrario a partir del punto al que hemos llamado 0. Así:

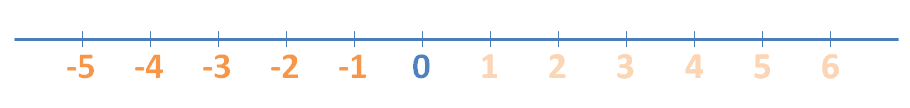
Recta dividida en segmentos unidad con números enteros negativos ubicados a la izquierda del punto 0.

Ubicar números racionales (Q) en la recta numérica:

Los siguientes son los números racionales (Q), que incluyen a los enteros y los naturales además de los decimales, son todos aquellos que se pueden expresar en forma de fracción.

Es muy fácil: el denominador de la fracción expresa en cuántas partes iguales tenemos que dividir la unidad y, el numerador, en cuál de esos puntos se localiza el número en la recta.

Por otro lado, si es positivo, se localizará a la derecha del 0 y si es negativo a la izquierda. Así:

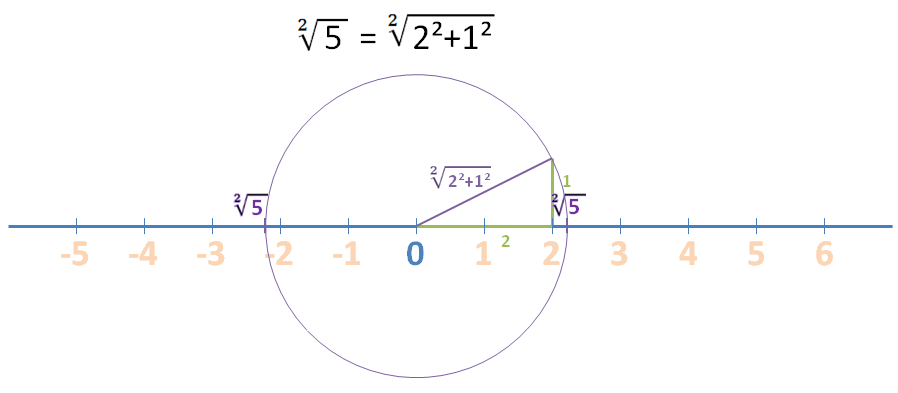
Entrada Relacionada: Teorema del resto

Ubicar números reales (R) en la recta numérica:

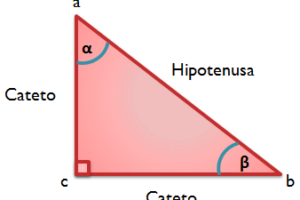
Representar el resto de números reales (R) es más complejo y se trabaja a partir de secundaria. Un buen recurso didáctico para la representación de las raíces cuadradas es el uso de triángulos rectángulos y circunferencias, explicándolo a partir del Teorema de Pitágoras y la propiedad de la circunferencia. Así: