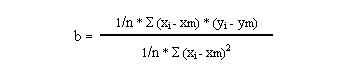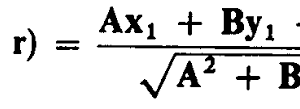Recta de regresión
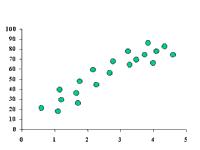
Representamos en un gráfico los pares de valores de una distribución bidimensional: la variable "x" en el eje horizontal o eje de las abcisas, y la variable "y" en el eje vertical o eje de las ordenadas. Vemos que la nube de puntos sigue una tendencia lineal:
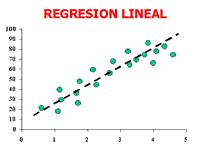
El coeficiente de correlación lineal nos permite determinar si, efectivamente, existe una relación entre las dos variables. Una vez que se concluye que existe una relación, la regresión nos permite definir la línea que mejor se ajusta a esta nube de puntos.
Una recta viene definida por la siguiente fórmula:
y = a + bx
Donde "y" sería la variable dependiente, es decir, la que se define a partir de la otra variable "x" (variable independiente). Para definir la línea es necesario determinar los valores de los parámetros "a" y "b":
El parámetro "a" es el valor que toma la variable dependiente "y", cuando la variable independiente "x" vale 0, y es el punto donde la línea cruza el eje vertical.
El parámetro "b" determina la pendiente de la línea, su grado de inclinación.
La regresión lineal nos permite calcular el valor de estos dos parámetros, definiendo la línea que mejor se ajusta a esta nube de puntos.
El parámetro "b" está determinado por la siguiente fórmula:
Es la covarianza de las dos variables, dividida por la varianza de la variable "x".
El parámetro "a" viene determinado por:
a = ym - (b * xm)
Es la media de la variable "y", menos la media de la variable "x" multiplicada por el parámetro "b" que hemos calculado.