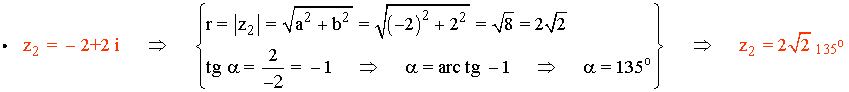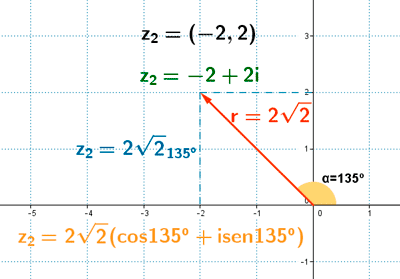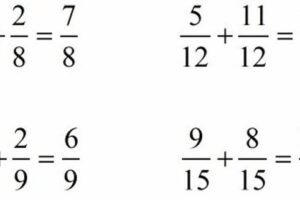
Representación polar de números complejos
El módulo de un número complejo z es el módulo del vector determinado por el origen del sistema de referencia y su afijo.
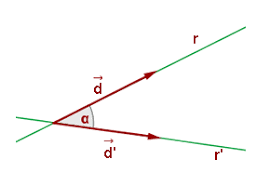
El argumento de un número complejo z es el ángulo que el vector
que corresponde a la forma del eje real semipositivo. Es decir, observando la figura anterior:
Argumento de z=α
Por lo tanto, estas tres formas de escribir un número complejo z son equivalentes:
- En la forma de un par: z=(a,b)
- En forma de binomio: z=a+bi
- En forma polar: z=rα
Cabe señalar que un mismo número complejo, escrito en forma polar, tiene un número ilimitado de argumentos: todos los ángulos que difieren en un número entero de "vueltas". Por lo tanto, el número complejo en forma polar debe escribirse z=rα+2kπ o z=rα+360oπ.
Sin embargo, se acostumbra a escribir z=rα, siendo α el llamado argumento principal. Así, el argumento principal es un ángulo entre 0∘ y 360∘.
Forma polar de un número complejo representación gráfica ejercicios resueltos
-1 es la tangente de 135o y de 315o . Observando la representación gráfica de z2 o su afijo (-2, 2)
vemos que está en el segundo cuadrante, por lo tanto el ángulo α es 135o .
Contenido