Funciones de segundo grado
Como sabemos, estudiar una función es poder determinar cómo se comportará gráficamente, sin necesidad de hacer una representación gráfica exhaustiva, punto por punto a partir de una tabla de valores.
En el caso del estudio de una función de segundo grado (también llamada cuadrática), tenemos un esquema de trabajo muy claro que implica llevar a cabo, en este orden, el estudio de los siguientes puntos que explicaré de forma sintética:
Concavidad
En palabras simples, es determinar cómo será la curvatura de la parábola. Está condicionado a conocer el signo del coeficiente del término de segundo grado, que solemos llamar
Si a > 0 la función tiene una concavidad positiva, y decimos que "sonríe" aludiendo al hecho de que la parábola que la representa parece una sonrisa (es una ayuda para la memoria que puede no gustarle a tu profesor..., tenlo en cuenta).
Si a < 0 la función tiene una concavidad negativa y decimos que "se enfada" aludiendo al hecho de que la parábola parece una mueca de enfado
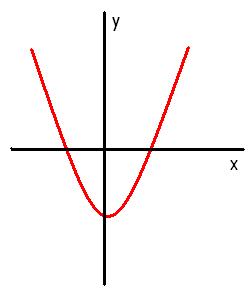
La siguiente imagen ilustra un caso de concavidad positiva:
Ordenado en el origen
Al calcular la ordenada al origen, estamos indicando el punto de corte con el eje de la ordenada o el eje vertical. Se encuentra sustituyendo 0 (cero) por las x que se ven en la expresión de la función, que se conoce comúnmente como "x-nula".
Raíces o soluciones
Revelan el punto o puntos de corte de la gráfica de funciones con el eje horizontal o de abscisas. Se calculan convirtiendo la función en una ecuación (igualándola a cero) y resolviéndola. Esa o esas soluciones -que pueden ser iguales entre sí o incluso no existir- son los puntos de corte que estás buscando.
Vértice
Representa el punto "más alto" de la curva si tiene una concavidad negativa (entonces decimos que es un máximo) o el punto "más bajo" si es una curva con una concavidad positiva (entonces decimos que es un mínimo).
Cuando se busca el vértice lo que se busca es un punto, y lo que se busca son sus coordenadas para ubicarlo en el plano. La coordenada x del vértice (Vx está simbolizada) se encuentra con la fórmula Vx= -b /2a; la coordenada y es sustityuendo ese valor de Vx que encontraste antes, en cada lugar donde x aparece en la expresión de la función; el resultado es la coordenada "y" del vértice.
Ejemplo de representación de una función cuadrática
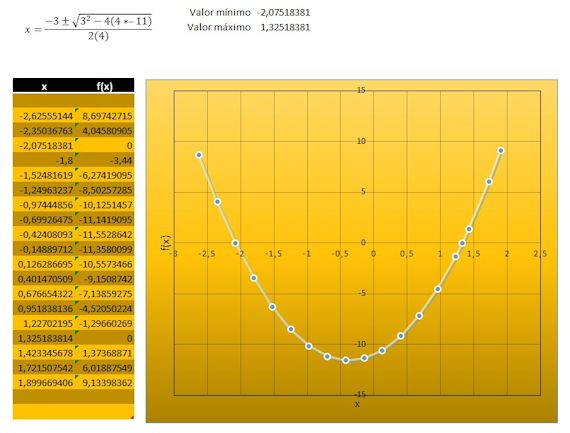
Calcular la función, la tabla y el gráfico para la ecuación 4x2 + 3x –5 = 6
Comenzamos por hacer que el resultado de la ecuación sea igual a cero:
Restamos 6 en ambos lados: 4x2 + 3x –5 –6 = 6 –6
Obtenemos 4x2 + 3x –11 = 0
Contenido