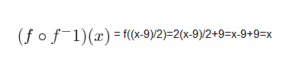Ejercicios de funciones compuestas

Una función compuesta es una función que está formada por la composición de dos funciones, es decir, la función que resulta de aplicar una función a x primero y luego de este resultado aplicamos una nueva función. La forma en que denominamos la función compuesta es un pequeño círculo entre las dos funciones o g(f(x)), lo que significa que primero se aplica la función f, y al resultado la función g.

Funciones compuestas

La función compuesta es la que se obtiene mediante una operación denominada composición de funciones, que consiste en aplicar sucesivamente las funciones que forman parte de la operación. Así pues, la función compuesta de f(x) y g(x) es otra función obtenida aplicando g a las imágenes de f.

Propiedades

La composición de funciones es asociativa, es decir:

$<img decoding="async" class="alignnone" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/54241bc77220479e208a59d88e5eca826086ab97" alt="" width="184" height="23" aria-hidden="true" />$

La composición de funciones en general no es conmutativa, es decir:

$<img decoding="async" class="alignnone" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9fac2baf1f3a00858a69ace217c4374e9314c8b1" alt="" width="127" height="23" aria-hidden="true" />$

Por ejemplo, dadas las funciones numéricas f(x)=x+1 y g(x)=x², entonces f(g(x))=x²+1, en tanto que g(f(x))=(x+1)².

El elemento neutro asociado a la composición de las funciones es la función de identidad.
Con las tres propiedades anteriores: elemento asociativo, no conmutativo y neutro, las funciones reales de la variable real constituyen un monoide para el funcionamiento interno de la composición de la función.
Además, el inverso de la composición de dos funciones es:

$<img decoding="async" class="alignnone aligncenter" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/aa7feda06bf3a320235c07b30a97fb226f693183" alt="" width="169" height="25" aria-hidden="true" />$

¿Cómo se calcula?

Para realizar la composición propiamente dicha de dos funciones ilustramos el proceso con el ejemplo con el que abríamos el apartado: siendo f(x)=x² y g(x)=x+2, podemos calcular (g∘f)(x) sin más que sustituir f(x) en los lugares donde pone x en g(x), es decir:

$(g \circ f) (x) = g [f (x)] = g (x 2) = x + 2 x \Rightarrow x 2 = x 2 + 2$

Funciones compuestas

Dadas las siguientes funciones f(x)=2x+9 y g(x)=1- 3/x, realizar las siguientes composiciones indicadas:
a) Hallar (g∘ f).
b) Hallar (f∘ g).
c) Sabiendo que la inversa de f es (x-9)/2, comprobar que se cumple la propiedad número 4.

Entrada Relacionada: Buscarv en excel

a) La composición de f y g:

(g∘ f)(x)=g(f(x))=g(2x+9)=1-3/(2x+9)

Como podéis observar, en primer lugar sustituimos el valor de f(x), y a continuación, hemos sustituido el valor de x en la función g por el valor de f(x).

b) Siguiendo el mismo procedimiento calculamos ahora g compuesto con f:

(f∘ g)(x)=f(g(x))=f(1-3/x)=2(1-3/x)+9=2-6/x+9=11-6/x

Como podemos ver, es distinta a la calculada en el apartado a, como era de esperar, ya que no son conmutativas.

c) Calculamos ahora la composición de f con su inversa: