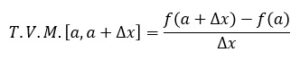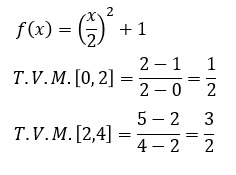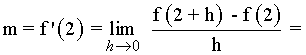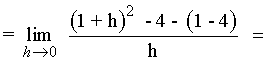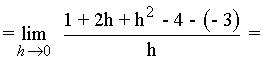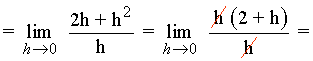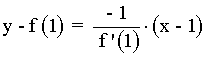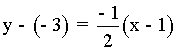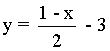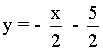
Interpretación geométrica de la derivada
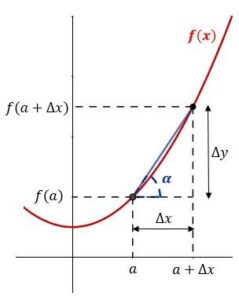
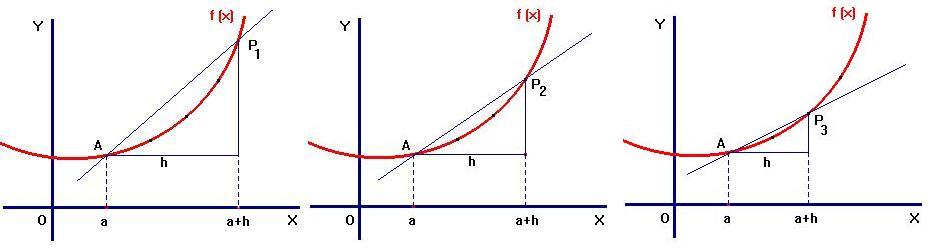
La fórmula anterior para la tasa media de variación (TMA) corresponde a la pendiente de la línea que conecta los puntos de la función a-y a-abscisa, a + Δ x, es decir, la tangente del ángulo α:
O, lo que es lo mismo:
Si hacemos Δ x cada vez más pequeña, de modo que tiende a cero, los puntos de la función de la abscisa a y a, a + Δx tienden a confundirse en un punto.
De esta manera, la recta secante anterior del límite se convierte en la tangente de la gráfica de la función en (a, f(a)), es decir, la tangente del ángulo α:
Conociendo la derivada, o lo que es lo mismo, la tangente del ángulo que forma la recta tangente, puedes obtener la ecuación de esta recta, como verás en el ejercicio.
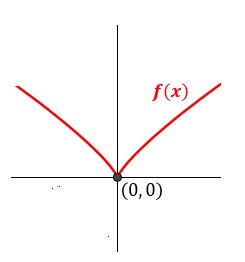
Esta interpretación geométrica de la derivada ilustra la no derivación en un punto angular, como en el caso, el (0, 0) de la imagen, punto en el que no se puede dibujar una sola tangente. No hay ninguna derivada en ese punto.
Como se ha dicho, la derivada f'(a) es la tasa de variación instantánea en ese punto: T.V.I.(a).
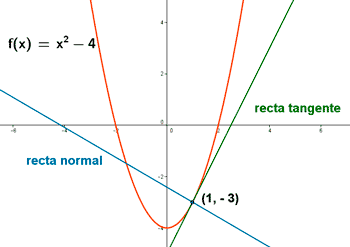
Ejemplo de Interpretación geométrica de la derivada
Calcula las ecuaciones de las rectas tangente y normal a la curva f(x) = x2 - 4 en el punto (1, -3)
Y la ecuación de la recta normal:
Contenido