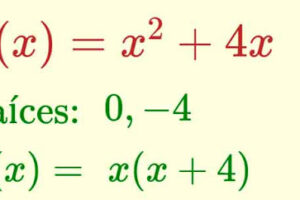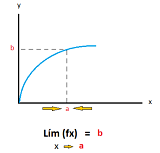
Limites de una función

Límites de una función

Las funciones matemáticas se utilizan en otras áreas, por ejemplo, para calcular los beneficios o costes de una empresa, la velocidad o aceleración de un móvil, etc., por lo que es importante conocer el comportamiento de una función. Las funciones nos ayudan a visualizar la gráfica de la función, los límites también se utilizan para estudiar otras propiedades, como la continuidad de una función, la diferenciabilidad, etc.

¿Qué es el límite de una función?

Se dice que una función f (x) tiene límite L en el punto x = a, si es posible aproximar f (x) a L tanto como se quiera cuando x se aproxima indefinidamente a a, siendo diferente de a. En términos matemáticos, se expresa como:

Dado el punto a, y de acuerdo con la definición anterior, hay dos maneras de aproximar x a a: a partir de valores x > a (desde la derecha) y a partir de valores x < a (desde la izquierda). En cada caso se obtienen valores denominados límite derecho (x®a+) y límite izquierdo (x®a-). Por definición, para que exista el límite de una función, deben cumplirse los dos límites laterales (derecho e izquierdo) y ambos deben ser iguales. Esto se expresa como:

Cómo resolver el límite de una función

Para resolver el límite de una función hay que tener en cuenta las propiedades de los mismos:

Dadas dos funciones f(x) y g(x) que tienen un límite en un punto a, se cumplen las siguientes propiedades:

El límite de la suma de ambas funciones es igual a la suma de los límites.
El límite de la diferencia se calcula como la diferencia de los límites.
El límite del producto de las funciones es igual al producto de sus límites.
El límite del cociente entre ambas funciones es igual al cociente entre los límites, siempre que el límite del denominador sea diferente de cero.
El límite del producto de una constante por una función se determina por la multiplicación de la constante por el límite de la función.

Entrada Relacionada: Ejemplos de movimiento rectilíneo uniforme

Estas propiedades se expresan matemáticamente de la siguiente manera:

Límites laterales

Una función tiene un límite si los dos límites laterales existen y coinciden.

El límite de una función f(x) en a, si existe, este límite es único.

Los valores de x pueden darse cada vez más cerca de a a a la izquierda o a la derecha. Obtendremos el límite lateral de la izquierda, que llamaremos L1 y/o el límite lateral de la derecha, que llamaremos L2.

Por lo tanto, para que exista el límite L de una función f(x) en a, si existe, el límite de la izquierda y el de la derecha deben ser iguales, L1 = L2.

Veamos esta función:

Queremos averiguar si existe el límite cuando x → 1.

Límite cuando x tiende a 1 en el ejemplo 1 de límites laterales
Si sustituimos el valor de x por 1 llegamos a una indeterminación del tipo número partido por cero que requiere operaciones posteriores.

Vamos, pues, a hallar sus límites laterales, dando en primer lugar valores a x cada vez más próximos a 1, pero menores que 1 (nos acercamos a 1 por la izquierda).