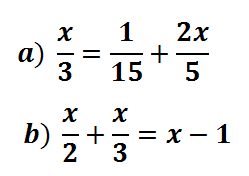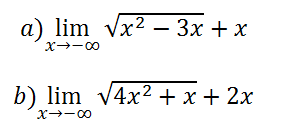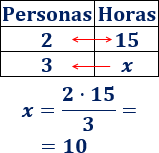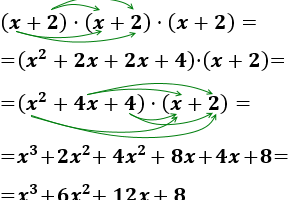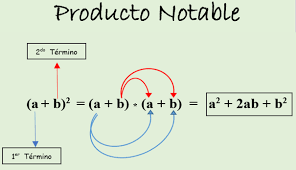
Productos notables fórmulas

Ciertos productos que cumplen con reglas fijas y cuyo resultado se puede anotar sin comprobar la multiplicación se denominan productos notables.

¿Cómo resolvemos un producto notable?

Para ello, debemos saber que, al igual que los números reales, las expresiones algebraicas pueden expresarse como poder. Así, si el exponente es un número natural, la potencia será una expresión algebraica completa.

(x2+2)2

Binomio al cuadrado

Es la multiplicación de un binomio por sí mismo, expresada en forma de potencia, donde los términos se suman o se restan:

a. Binomio de suma al cuadrado: es igual al cuadrado del primer término, más dos veces el producto de los términos, más el cuadrado del segundo término. Se expresa de la siguiente manera:

(a + b)2 = (a + b) * (a + b)

Producto de los binomios conjugados

Se conjugan dos binomios cuando los segundos términos de cada uno son de signos diferentes, es decir, el primero es positivo y el segundo negativo o viceversa. Se resuelve elevando cada monomio al cuadrado y restándolos. Su fórmula es la siguiente:

(a + b) * (a - b)

Producto de dos binomios con un término común

Es uno de los productos más complejos y raramente utilizados, porque es una multiplicación de dos binomios que tienen un término en común. La regla indica lo siguiente:

El cuadrado del término común.
Además suma los términos que no son comunes y luego los multiplica por el término común.
Más la suma de la multiplicación de los términos que no son comunes.
Se representa en la fórmula: (x + a) * (x + b) y se desarrolla como se muestra en la imagen. El resultado es un trinomio cuadrado no perfecto.

Entrada Relacionada: Fórmulas de integrales

Polinomio al cuadrado

En este caso hay más de dos términos y para desarrollarlo, cada uno se cuadra y se suma con el doble de la multiplicación de un término por otro; su fórmula es: (a + b + c)2 y el resultado de la operación es un trinomio al cuadrado.