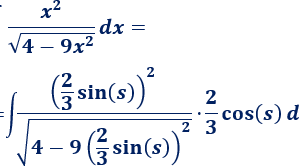
¿Qué es una función?
Una función es una relación entre dos magnitudes o cantidades, por ejemplo x y f(x), de manera que cada valor de la primera magnitud llamado vista previa corresponde a un único valor de la segunda, llamado imagen.
Se dirá que la primera magnitud o vista previa es la variable independiente y la segunda magnitud o imagen (que se deduce de la primera) será la variable dependiente. Por ejemplo, si la variable independiente es x, la variable dependiente será f (x), que se lee "f de x", que suele designarse con la letra y. Entonces se dirá que y es una función de x, o que y depende de x.
El conjunto inicial o de inicio donde se encuentran las previsualizaciones se denomina dominio que se abrevia Dom (f) y el conjunto final o de llegada donde las imágenes se denominan codoma que se abrevia Codom (f).
El conjunto de todas las imágenes de una función se llama camino (o rango) y se abrevia Rec (f). El camino es un subconjunto del conjunto final del codominio, en el que puede ser que el camino sea un conjunto más pequeño que el codominio o que el camino coincida exactamente con el codominio.
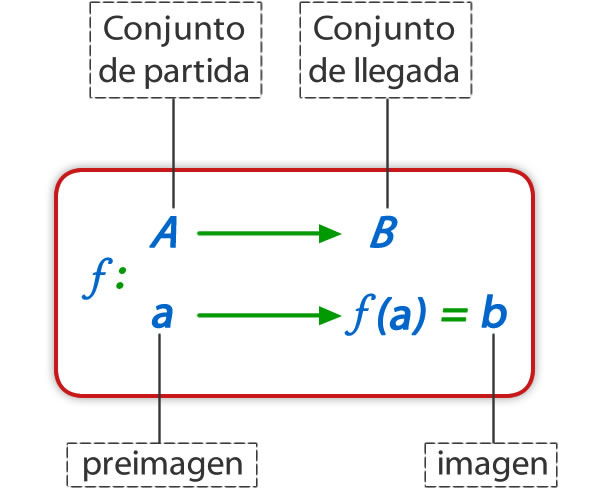
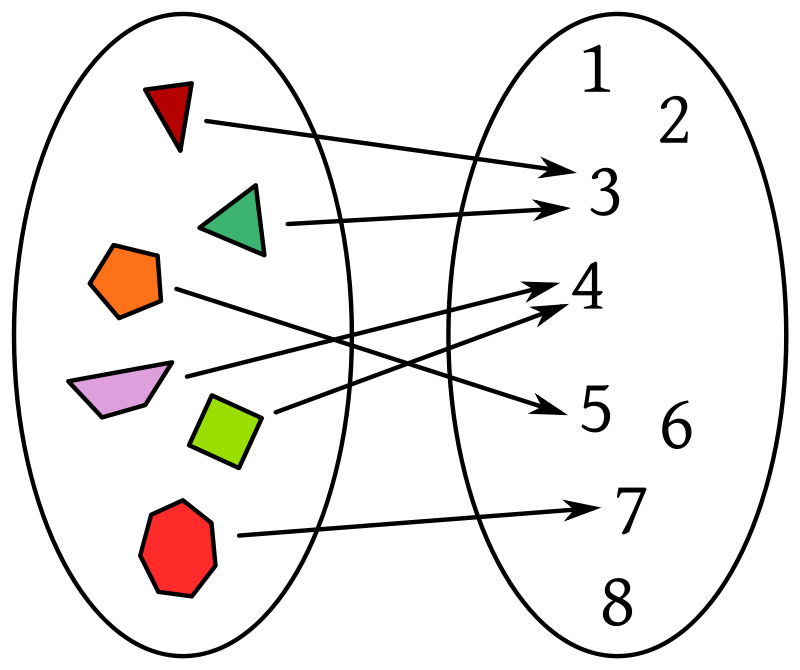
Por ejemplo, para una función f de un conjunto A en un conjunto B, podemos representarla matemáticamente de la siguiente manera:
Aquí podemos ver cómo f (a) representa la transformación del elemento a por la función f que da lugar al elemento b. Se dirá que a es la imagen previa de b, o viceversa, b o f (a) es la imagen de a cuando es procesada por f.
Tipos de funciones
- Lineal: f(x) = a*x + b;
- Cuadrática: f(x) = a*x^2 + b*x + c;
- Funciones de la raíz: f(x) = sqrt(k*x)
- Funciones de proporcionalidad inversa: f(x) = k/x
- Funciones exponenciales: f(x) = a^x;
- Funciones logarítmicas: f(x) = log(x);
- Funciones trigonométricas: f(x) = sin(x); f(x) = cos(x); f(x) = tan(x)
- Funciones del arco: f(x) = asin(x); f(x) = acos(x); f(x) = atan(x);
Contenido