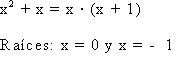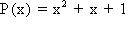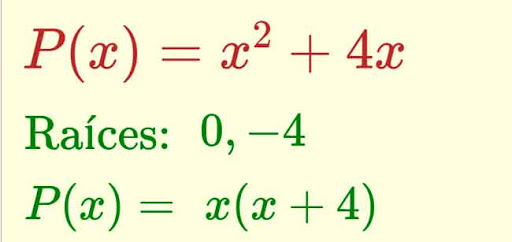
Raíces de polinomios

Las raíces de un polinomio son aquellos valores que, si los sustituimos por la variable «x», el resultado de la ecuación del polinomio es cero. Esto, dicho de forma más coloquial, puede expresarse como los valores de X para los que el polinomio vale cero.

Calcular Raíces de polinomios

Cuando resolvemos un polinomio igualándolo a cero obtenemos como soluciones las raíces del polinomio. Como propiedades de las raíces y factores de los polinomios podemos decir que los ceros o raíces de un polinomio son por los divisores del término independiente perteneciente al polinomio. Entonces a cada raíz del tipo x = a correspondería un binomio del tipo (x-a). Un polinomio puede expresarse en factores si lo escribimos como producto de todos los binomios que tenemos del tipo (x-a) que corresponden a las raíces, x=a, que obtenemos.

Ejemplos de cálculo de raíces de polinomios

Debemos tener en cuenta que la suma de los exponentes del binomio es igual al grado del polinomio, también tenemos en cuenta que cualquier polinomio que no tenga un término independiente admitirá como raíz x=0, de otra manera, admitirá como factor x. Por ejemplo: