Sumas de Riemann

Una suma de Riemann es una aproximación del área bajo la curva, dividiéndola en varias formas simples (como rectángulos o trapecios).

Tipos de sumas de Riemann

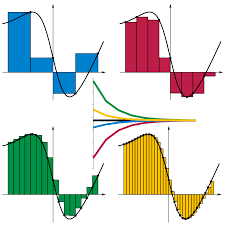
En una suma izquierda de Riemann aproximamos el área con rectángulos (normalmente de igual anchura), donde la altura de cada rectángulo es igual al valor de la función en el extremo izquierdo de su base. Se traza una función. El eje x no está numerado. El gráfico es una curva. La curva comienza en el eje y positivo, se mueve hacia arriba con una forma cóncava, y termina en el cuadrante 1. Se sombrea un área entre la curva y el eje x. El área sombreada se divide en 4 rectángulos de la misma anchura que tocan la curva en la esquina superior izquierda.
En una suma de Riemann derecha, la altura de cada rectángulo es igual al valor de la función en el extremo derecho de su base. En el gráfico de la función, la región debajo de la curva se divide en 4 rectángulos con la misma anchura que tocan la curva en el ángulo superior derecho.
En una suma del punto medio de Riemann, la altura de cada rectángulo es igual al valor de la función en el punto medio de su base. En el gráfico de la función, la región debajo de la curva se divide en 4 rectángulos con la misma anchura que tocan la curva en los puntos medios de los lados superiores.
También podemos utilizar los trapecios para aproximar el área (esto se llama regla trapezoidal). En este caso, cada trapezoide toca la curva en sus dos vértices superiores.
En el gráfico de la función, la región debajo de la curva se divide en 4 trapecios con la misma anchura que tocan la curva en el vértice superior.

Entrada Relacionada: Representación polar de números complejos

Para cada tipo de aproximación, cuantas más formas utilicemos, más cercana será la aproximación al área real.
Las referencias difieren en este punto, pero llamamos suma de Riemann a cualquier aproximación que utilice rectángulos y suma trapezoidal a cualquier aproximación que utilice trapezoides.

El área bajo la curva

La principal propiedad de la suma de Riemann, y de la cual proviene su importancia, es que si el número de subdivisiones tiende al infinito, el resultado de la suma converge en la integral definida de la función: