Teorema del valor intermedio
En otras palabras, una función continua toma todos los valores entre ![]() y
y ![]() cuando los valores de
cuando los valores de ![]() cambian desde
cambian desde ![]() hasta
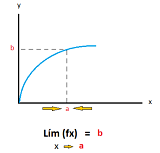
hasta ![]() . La siguiente gráfica muestra esto de una manera más clara:
. La siguiente gráfica muestra esto de una manera más clara:

Cuando el valor k va subiendo, los valores de ![]() van moviéndose hacia la derecha (para la gráfica de la función mostrada) y cuando k va bajando sobre el eje y, los valores de
van moviéndose hacia la derecha (para la gráfica de la función mostrada) y cuando k va bajando sobre el eje y, los valores de ![]() van moviéndose hacia la izquierda. Geométricamente este teorema nos dice que la línea horizontal y = k corta a la gráfica de la función y = f(x) en al menos un punto cuando es continua en el intervalo
van moviéndose hacia la izquierda. Geométricamente este teorema nos dice que la línea horizontal y = k corta a la gráfica de la función y = f(x) en al menos un punto cuando es continua en el intervalo ![]() y se cumple que
y se cumple que ![]() y
y ![]() .
.
Es posible que corte a la gráfica de la función en varios puntos. Por ejemplo, si dibujamos el punto ![]() después del máximo que se dibujó, es posible para algunos puntos de la gráfica que la recta horizontal corte en dos de sus puntos.
después del máximo que se dibujó, es posible para algunos puntos de la gráfica que la recta horizontal corte en dos de sus puntos.
Teorema del valor medio ejemplos
Demuestra que la función:
![]()
tiene una raíz en el intervalo![]() .
.
Para eso vamos a aplicar el teorema del valor intermedio. Como la función es polinomial es continua en todo el conjunto de los números reales. Si ![]() para algún
para algún ![]() que está en el intervalo
que está en el intervalo ![]() , hacemos
, hacemos ![]() , y
, y ![]() , y evaluamos la función en esos puntos:
, y evaluamos la función en esos puntos:
![]()
Por lo que satisface con la condición de que ![]() . Entonces, por la continuidad de la función, debe existir un número
. Entonces, por la continuidad de la función, debe existir un número ![]() en el intervalo
en el intervalo ![]() tal que
tal que ![]() .
.
Nótese que no hemos dicho cómo calcular el valor de x0 que es la raíz de la función dada. Sólo sabemos que existe. Tampoco podemos asegurar que sea única.
En realidad este es el teorema que usamos cuando decimos que una función polinómica de grado impar tiene al menos una raíz real porque para valores positivos y grandes de x los valores devueltos por la función se vuelven positivos para alguna x suficientemente grande, y cuando x es negativa y muy grande, los valores devueltos por la función son negativos.
Entonces, dado que toda función polinómica es continua en todo el conjunto de números reales, si elegimos el intervalo [p,q\] con p de tal forma que f(p) es un número negativo y q de tal forma que f(q) es positivo, entonces, por el teorema del valor intermedio, hay un número x0 en el intervalo y satisface:
.
Contenido