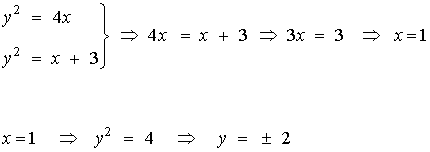Área entre las gráficas de funciones
La velocidad, la aceleración constante y muchos otros conceptos físicos y matemáticos pueden ser despejados con la ayuda del área bajo sus respectivas curvas.
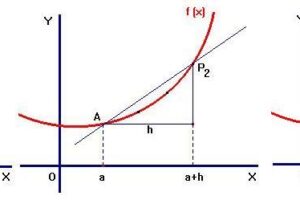
El primer paso en la base del concepto de integrales implica la formulación del área bajo el gráfico de una función.
El área aproximada bajo el gráfico de una función puede formularse representando un pequeño rectángulo de altura y anchura fijas que equivale al valor de la función en el medio del intervalo correspondiente.
Área = fi x
Aquí f(x) es la función de x. Hay que tener en cuenta que cuanto más pequeño sea el ancho del rectángulo, mejor será la aproximación.
El rectángulo puede ser un rectángulo interior o exterior. El área de todos los rectángulos se suma para obtener el área final bajo el gráfico de la función.
Para reducir el esfuerzo de sumar las áreas individuales de todos los rectángulos, se desarrolló el concepto de la integral definida.
El área bajo la gráfica de la función puede determinarse realizando las integrales definidas entre los puntos dados.
Área entre las gráficas de funciones ejercicios resueltos
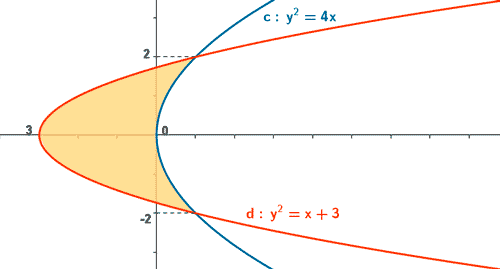
- Hallar el área limitada por las curvas y2 = 4x ; y2 = x + 3.
Empezamos por encontrar los puntos donde las dos curvas se cruzan
de manera que los puntos de intersección son ( 1, 2 ) y ( 1 , -2 ).
A la vista de la gráfica, el área pedida se calcula como sigue:
Contenido