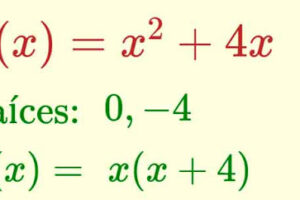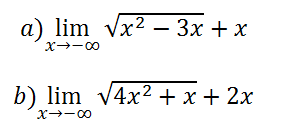Límites
En el cálculo (especialmente en el análisis real y matemático) este concepto se utiliza para definir los conceptos fundamentales de convergencia, continuidad, derivación, integración, entre otros. Aunque el concepto de límite parece intuitivamente relacionado con el concepto de distancia, en un espacio euclidiano, es el tipo de conjuntos abiertos inducidos por esta métrica, lo que permite definir rigurosamente la noción de límite.
El concepto puede generalizarse a otros espacios topológicos, como las redes topológicas; del mismo modo, se define y se utiliza en otras ramas de las matemáticas, como la teoría de las categorías.
Límites ejercicios
Hallar los siguientes límites cuando x → - ∞ :
Es suficiente con hacer el cambio en el término de mayor grado, que es el único que influye.
Dependiendo de si el exponente es par o impar, el resultado será positivo o negativo.
Contenido